Creating an IRDataCurve Object
To create an IRDataCurve object, see the
following options:
Use IRDataCurve with Dates and Data
Use IRDataCurve with vectors of dates
and data to create an interest-rate curve object. When constructing the
IRDataCurve object, you can also use optional inputs to
define how the interest-rate curve is constructed from the dates and data.
Example
In this example, you create the vectors for Dates and
Data for an interest-rate curve.
Data = [2.09 2.47 2.71 3.12 3.43 3.85 4.57 4.58]/100; Dates = daysadd(today,[360 2*360 3*360 5*360 7*360 10*360 20*360 30*360],1);
Use IRDataCurve to build
interest-rate objects based on the constant and
pchip interpolation methods.
irdc_const = IRDataCurve('Forward',today,Dates,Data,'InterpMethod','constant'); irdc_pchip = IRDataCurve('Forward',today,Dates,Data,'InterpMethod','pchip');
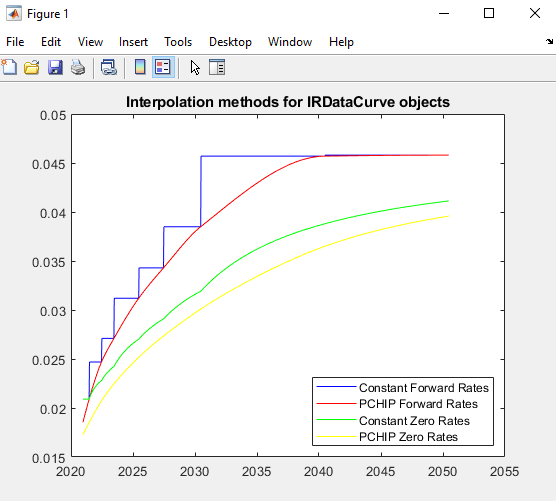
Plot the forward and zero rate curves for the two IRDataCurve objects based on
constant and pchip interpolation
methods.
PlottingDates = daysadd(today,180:10:360*30,1); plot(PlottingDates, getForwardRates(irdc_const, PlottingDates),'b') hold on plot(PlottingDates, getForwardRates(irdc_pchip, PlottingDates),'r') plot(PlottingDates, getZeroRates(irdc_const, PlottingDates),'g') plot(PlottingDates, getZeroRates(irdc_pchip, PlottingDates),'yellow') legend({'Constant Forward Rates','PCHIP Forward Rates','Constant Zero Rates',... 'PCHIP Zero Rates'},'location','SouthEast') title('Interpolation methods for IRDataCurve objects') datetick
The plot demonstrates the relationship of the forward and zero rate curves.
Bootstrap IRDataCurve Based on Market Instruments
Use the bootstrapping function, based on market instruments, to create an
interest-rate curve object. When bootstrapping, you also have the option to define a
range of interpolation methods (linear,
spline, constant, and
pchip).
Example 1
In this example, you bootstrap a swap curve from deposits, Eurodollar Futures
and swaps. The input market data for this example is hard-coded and specified as
two cell arrays of data; one cell array indicates the type of instrument and the
other contains the Settle, Maturity values
and a market quote for the instrument. For deposits and swaps, the quote is a
rate; for the EuroDollar futures, the quote is a price. Although bonds are not
used in this example, a bond would also be quoted with a price.
InstrumentTypes = {'Deposit';'Deposit';'Deposit';'Deposit';'Deposit'; ...
'Futures';'Futures'; ...
'Futures';'Futures';'Futures'; ...
'Futures';'Futures';'Futures'; ...
'Futures';'Futures';'Futures'; ...
'Futures';'Futures';'Futures'; ...
'Futures';'Futures';'Futures'; ...
'Swap';'Swap';'Swap';'Swap';'Swap';'Swap';'Swap'};
Instruments = [datenum('08/10/2007'),datenum('08/17/2007'),.0532063; ...
datenum('08/10/2007'),datenum('08/24/2007'),.0532000; ...
datenum('08/10/2007'),datenum('09/17/2007'),.0532000; ...
datenum('08/10/2007'),datenum('10/17/2007'),.0534000; ...
datenum('08/10/2007'),datenum('11/17/2007'),.0535866; ...
datenum('08/08/2007'),datenum('19-Dec-2007'),9485; ...
datenum('08/08/2007'),datenum('19-Mar-2008'),9502; ...
datenum('08/08/2007'),datenum('18-Jun-2008'),9509.5; ...
datenum('08/08/2007'),datenum('17-Sep-2008'),9509; ...
datenum('08/08/2007'),datenum('17-Dec-2008'),9505.5; ...
datenum('08/08/2007'),datenum('18-Mar-2009'),9501; ...
datenum('08/08/2007'),datenum('17-Jun-2009'),9494.5; ...
datenum('08/08/2007'),datenum('16-Sep-2009'),9489; ...
datenum('08/08/2007'),datenum('16-Dec-2009'),9481.5; ...
datenum('08/08/2007'),datenum('17-Mar-2010'),9478; ...
datenum('08/08/2007'),datenum('16-Jun-2010'),9474; ...
datenum('08/08/2007'),datenum('15-Sep-2010'),9469.5; ...
datenum('08/08/2007'),datenum('15-Dec-2010'),9464.5; ...
datenum('08/08/2007'),datenum('16-Mar-2011'),9462.5; ...
datenum('08/08/2007'),datenum('15-Jun-2011'),9456.5; ...
datenum('08/08/2007'),datenum('21-Sep-2011'),9454; ...
datenum('08/08/2007'),datenum('21-Dec-2011'),9449.5; ...
datenum('08/08/2007'),datenum('08/08/2014'),.0530; ...
datenum('08/08/2007'),datenum('08/08/2017'),.0545; ...
datenum('08/08/2007'),datenum('08/08/2019'),.0551; ...
datenum('08/08/2007'),datenum('08/08/2022'),.0559; ...
datenum('08/08/2007'),datenum('08/08/2027'),.0565; ...
datenum('08/08/2007'),datenum('08/08/2032'),.0566; ...
datenum('08/08/2007'),datenum('08/08/2037'),.0566];
bootstrap is called as a
function of the IRDataCurve object. Inputs to
this function include the curve Type (zero
or forward), Settle date,
InstrumentTypes, and Instrument data.
The bootstrap function also supports optional arguments,
including an interpolation method, compounding, basis, and an options structure
for bootstrapping. For example, you are passing in an IRBootstrapOptions object
which includes information for the ConvexityAdjustment to
forward rates.
IRsigma = .01; CurveSettle = datenum('08/10/2007'); bootModel = IRDataCurve.bootstrap('Forward', CurveSettle, ... InstrumentTypes, Instruments,'InterpMethod','pchip',... 'Compounding',-1,'IRBootstrapOptions',... IRBootstrapOptions('ConvexityAdjustment',@(t) .5*IRsigma^2.*t.^2))
bootModel = IRDataCurve Type: Forward Settle: 733264 (10-Aug-2007) Compounding: -1 Basis: 0 (actual/actual) InterpMethod: pchip Dates: [29x1 double] Data: [29x1 double]
The bootstrap function uses an Optimization Toolbox™ function to solve for any bootstrapped rates.
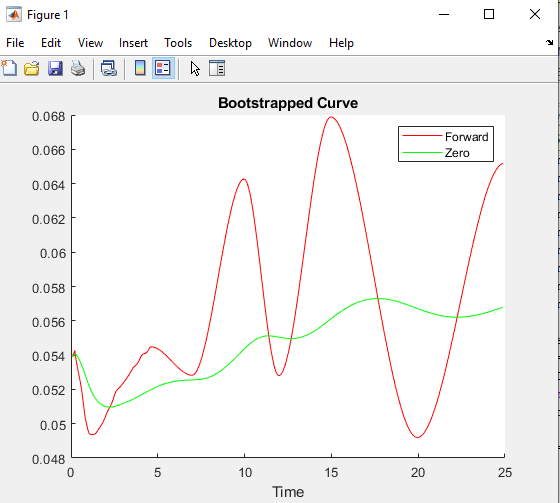
Plot the forward and zero curves.
PlottingDates = (CurveSettle+20:30:CurveSettle+365*25)'; TimeToMaturity = yearfrac(CurveSettle,PlottingDates); BootstrappedForwardRates = getForwardRates(bootModel, PlottingDates); BootstrappedZeroRates = getZeroRates(bootModel, PlottingDates); figure hold on plot(TimeToMaturity,BootstrappedForwardRates,'r') plot(TimeToMaturity,BootstrappedZeroRates,'g') title('Bootstrapped Curve') xlabel('Time') legend({'Forward','Zero'})
The plot demonstrates the forward and zero rate curves for the market data.
Example 2
In this example, you bootstrap a swap curve from deposits, Eurodollar futures,
and swaps. The input market data for this example is hard-coded and specified as
two cell arrays of data; one cell array indicates the type of instrument and the
other cell array contains the Settle,
Maturity values and a market quote for the instrument.
This example of bootstrapping also demonstrates the use of an
InstrumentBasis for each Instrument
type.
InstrumentTypes = {'Deposit';'Deposit';...
'Futures';'Futures';'Futures';'Futures';'Futures';'Futures';...
'Swap';'Swap';'Swap';'Swap';};
Instruments = [datenum('08/10/2007'),datenum('09/17/2007'),.0532000; ...
datenum('08/10/2007'),datenum('11/17/2007'),.0535866; ...
datenum('08/08/2007'),datenum('19-Dec-2007'),9485; ...
datenum('08/08/2007'),datenum('19-Mar-2008'),9502; ...
datenum('08/08/2007'),datenum('18-Jun-2008'),9509.5; ...
datenum('08/08/2007'),datenum('17-Sep-2008'),9509; ...
datenum('08/08/2007'),datenum('17-Dec-2008'),9505.5; ...
datenum('08/08/2007'),datenum('18-Mar-2009'),9501; ...
datenum('08/08/2007'),datenum('08/08/2014'),.0530; ...
datenum('08/08/2007'),datenum('08/08/2019'),.0551; ...
datenum('08/08/2007'),datenum('08/08/2027'),.0565; ...
datenum('08/08/2007'),datenum('08/08/2037'),.0566];
CurveSettle = datenum('08/10/2007');
The bootstrap function is called
as a function of the IRBootstrapOptions object.
Inputs to the bootstrap function include
the curve Type (zero or
forward), Settle date,
InstrumentTypes, and Instrument data.
The bootstrap function also supports optional arguments,
including an interpolation method, compounding, basis, and an options structure
for bootstrapping. In this example, you are passing an additional
Basis value for each instrument type.
bootModel=IRDataCurve.bootstrap('Forward',CurveSettle,InstrumentTypes, ... Instruments,'InterpMethod','pchip','InstrumentBasis',[repmat(2,8,1);repmat(0,4,1)])
bootModel = IRDataCurve Type: Forward Settle: 733264 (10-Aug-2007) Compounding: 2 Basis: 0 (actual/actual) InterpMethod: pchip Dates: [12x1 double] Data: [12x1 double]
The bootstrap function uses an Optimization Toolbox function to solve for any bootstrapped rates.
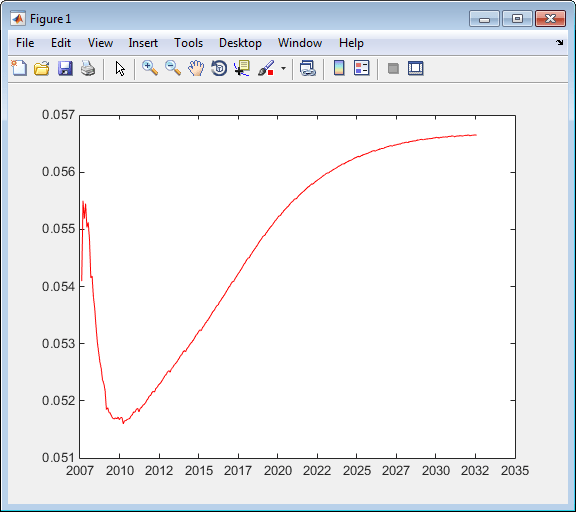
Plot the par yields curve using the getParYields
function.
PlottingDates = (datenum('08/11/2007'):30:CurveSettle+365*25)'; plot(PlottingDates, getParYields(bootModel, PlottingDates),'r') datetick
The plot demonstrates the par yields curve for the market data.
See Also
IRBootstrapOptions | IRDataCurve | IRFunctionCurve | IRFitOptions
Related Examples
- Creating Interest-Rate Curve Objects
- Bootstrapping a Swap Curve
- Dual Curve Bootstrapping
- Creating an IRFunctionCurve Object
- Fitting Interest-Rate Curve Functions
More About
- Interest-Rate Curve Objects and Workflow
- Mapping Financial Instruments Toolbox Curve Functions to Object-Based Framework
