cross
Cross product
Description
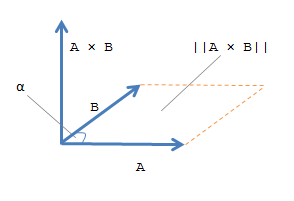
C = cross( returns the cross product of
A,B)A and B.
If
AandBare vectors, then they must have a length of 3.If
AandBare matrices or multidimensional arrays, then they must have the same size. In this case, thecrossfunction treatsAandBas collections of three-element vectors. The function calculates the cross product of corresponding vectors along the first array dimension whose size equals 3.
Examples
Input Arguments
More About
Extended Capabilities
Version History
Introduced before R2006a