Lognormal Distribution
Overview
The lognormal distribution, sometimes called the Galton distribution, is a probability distribution whose logarithm has a normal distribution. The lognormal distribution is applicable when the quantity of interest must be positive, because log(x) exists only when x is positive.
Statistics and Machine Learning Toolbox™ offers several ways to work with the lognormal distribution.
Create a probability distribution object
LognormalDistributionby fitting a probability distribution to sample data (fitdist) or by specifying parameter values (makedist). Then, use object functions to evaluate the distribution, generate random numbers, and so on.Work with the lognormal distribution interactively by using the Distribution Fitter app. You can export an object from the app and use the object functions.
Use distribution-specific functions (
logncdf,lognpdf,logninv,lognlike,lognstat,lognfit,lognrnd) with specified distribution parameters. The distribution-specific functions can accept parameters of multiple lognormal distributions.Use generic distribution functions (
cdf,icdf,pdf,random) with a specified distribution name ('Lognormal') and parameters.
Parameters
The lognormal distribution uses these parameters.
| Parameter | Description | Support |
|---|---|---|
mu (μ) | Mean of logarithmic values | |
sigma (σ) | Standard deviation of logarithmic values |
If X follows the lognormal distribution with parameters µ and σ, then log(X) follows the normal distribution with mean µ and standard deviation σ.
Parameter Estimation
To fit the lognormal distribution to data and find the parameter estimates,
use lognfit, fitdist, or mle.
For uncensored data,
lognfitandfitdistfind the unbiased estimates of the distribution parameters, andmlefinds the maximum likelihood estimates.For censored data,
lognfit,fitdist, andmlefind the maximum likelihood estimates.
Unlike lognfit and mle,
which return parameter estimates, fitdist returns the
fitted probability distribution object LognormalDistribution. The object
properties mu and sigma store the
parameter estimates.
Descriptive Statistics
The mean m and variance v of a lognormal random variable are functions of the lognormal distribution parameters µ and σ:
Also, you can compute the lognormal distribution parameters µ and σ from the mean m and variance v:
Probability Density Function
The probability density function (pdf) of the lognormal distribution is
For an example, see Compute Lognormal Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the lognormal distribution is
For an example, see Compute Lognormal Distribution cdf.
Examples
Compute Lognormal Distribution pdf
Suppose the income of a family of four in the United States follows a lognormal distribution with mu = log(20,000) and sigma = 1. Compute and plot the income density.
Create a lognormal distribution object by specifying the parameter values.
pd = makedist('Lognormal','mu',log(20000),'sigma',1)
pd =
LognormalDistribution
Lognormal distribution
mu = 9.90349
sigma = 1
Compute the pdf values.
x = (10:1000:125010)'; y = pdf(pd,x);
Plot the pdf.
plot(x,y)
h = gca;
h.XTick = [0 30000 60000 90000 120000];
h.XTickLabel = {'0','$30,000','$60,000',...
'$90,000','$120,000'};
Compute Lognormal Distribution cdf
Compute the cdf values evaluated at the values in x for the lognormal distribution with mean mu and standard deviation sigma.
x = 0:0.2:10; mu = 0; sigma = 1; p = logncdf(x,mu,sigma);
Plot the cdf.
plot(x,p) grid on xlabel('x') ylabel('p')

Relationship Between Normal and Lognormal Distributions
If X follows the lognormal distribution with parameters µ and σ, then log(X) follows the normal distribution with mean µ and standard deviation σ. Use distribution objects to inspect the relationship between normal and lognormal distributions.
Create a lognormal distribution object by specifying the parameter values.
pd = makedist('Lognormal','mu',5,'sigma',2)
pd =
LognormalDistribution
Lognormal distribution
mu = 5
sigma = 2
Compute the mean of the lognormal distribution.
mean(pd)
ans = 1.0966e+03
The mean of the lognormal distribution is not equal to the mu parameter. The mean of the logarithmic values is equal to mu. Confirm this relationship by generating random numbers.
Generate random numbers from the lognormal distribution and compute their log values.
rng('default'); % For reproducibility x = random(pd,10000,1); logx = log(x);
Compute the mean of the logarithmic values.
m = mean(logx)
m = 5.0033
The mean of the log of x is close to the mu parameter of x, because x has a lognormal distribution.
Construct a histogram of logx with a normal distribution fit.
histfit(logx)
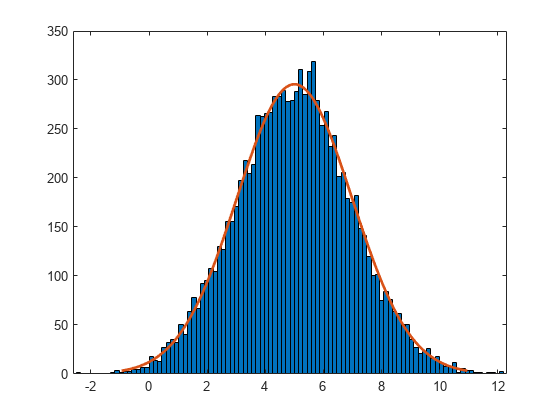
The plot shows that the log values of x are normally distributed.
histfit uses fitdist to fit a distribution to data. Use fitdist to obtain parameters used in fitting.
pd_normal = fitdist(logx,'Normal')pd_normal =
NormalDistribution
Normal distribution
mu = 5.00332 [4.96445, 5.04219]
sigma = 1.98296 [1.95585, 2.01083]
The estimated normal distribution parameters are close to the lognormal distribution parameters 5 and 2.
Compare Lognormal and Burr Distribution pdfs
Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution.
Generate the income data.
rng('default') % For reproducibility y = random('Lognormal',log(25000),0.65,[500,1]);
Fit a Burr distribution.
pd = fitdist(y,'burr')pd =
BurrDistribution
Burr distribution
alpha = 26007.2 [21165.5, 31956.4]
c = 2.63743 [2.3053, 3.0174]
k = 1.09658 [0.775479, 1.55064]
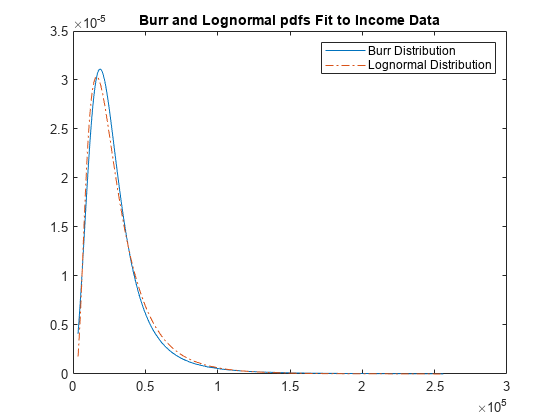
Plot both the Burr and lognormal pdfs of income data on the same figure.
p_burr = pdf(pd,sortrows(y)); p_lognormal = pdf('Lognormal',sortrows(y),log(25000),0.65); plot(sortrows(y),p_burr,'-',sortrows(y),p_lognormal,'-.') title('Burr and Lognormal pdfs Fit to Income Data') legend('Burr Distribution','Lognormal Distribution')
Related Distributions
Normal Distribution — The lognormal distribution is closely related to the normal distribution. If X is distributed lognormally with parameters μ and σ, then log(x) is distributed normally with mean μ and standard deviation σ. See Relationship Between Normal and Lognormal Distributions.
Burr Type XII Distribution — The Burr distribution is a flexible distribution family that can express a wide range of distribution shapes. It has as a limiting case many commonly used distributions such as gamma, lognormal, loglogistic, bell-shaped, and J-shaped beta distributions (but not U-shaped). See Compare Lognormal and Burr Distribution pdfs.
References
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.
[3] Lawless, J. F. Statistical Models and Methods for Lifetime Data. Hoboken, NJ: Wiley-Interscience, 1982.
[4] Marsaglia, G., and W. W. Tsang. “A Fast, Easily Implemented Method for Sampling from Decreasing or Symmetric Unimodal Density Functions.” SIAM Journal on Scientific and Statistical Computing. Vol. 5, Number 2, 1984, pp. 349–359.
[5] Meeker, W. Q., and L. A. Escobar. Statistical Methods for Reliability Data. Hoboken, NJ: John Wiley & Sons, Inc., 1998.
[6] Mood, A. M., F. A. Graybill, and D. C. Boes. Introduction to the Theory of Statistics. 3rd ed., New York: McGraw-Hill, 1974. pp. 540–541.
See Also
LognormalDistribution | logncdf | lognpdf | logninv | lognlike | lognstat | lognfit | lognrnd
